Estimating Pi Using a Dartboard
I. Introduction
This is a fun demonstration of how Pi can be found seemingly out of nowhere. What I am about to show is a popularior simulation of a Monte Carlo method. Monteo Carlo methods are general computational algorithms that rely on repeated random sampling as a way to try to extract valueable information. For this demonstration, we are going to try to to get an estimation for the value of Pi using nothing but a dartboard.
We will begin by first showing the demonstration, and then going over some of the math behind it.
II. The Demonstration
To begin, we will imagine that in front of us we have a standard dartboard. For our purposes, we do not
care about the points associated within the dartboard, we only care about the circular shape of it. Furthermore,
we will assume that our dartboard is perfectly inscribed within a square.
From here, we are going to throw a bunch of darts at the board and hope it hits. Unfortunately for us, we have
terrible coordination so the location where the dart dies is going to be completely random.
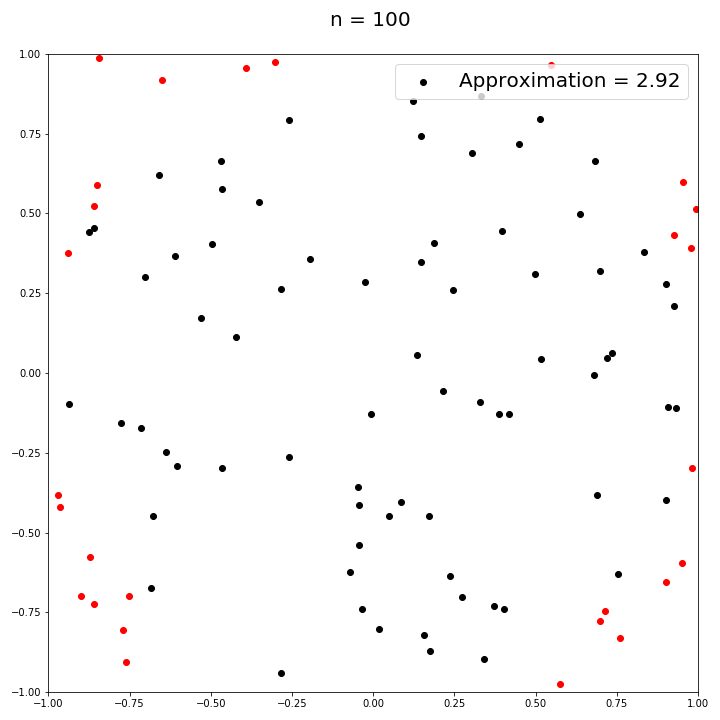
Let's throw 100 darts and mark the ones that land on the board in black, and those that miss the board
completely in red.
Next, we will go ahead and divide the number of misses by the total number of throws and
multiple that value by four for seemingly no reason.
\[4~*~\frac{\#~of~Misses}{Total}\]
Given this is a relatively small number, we
can go ahead and count the values ourselves. We see that we have 73 hits out of 100 attempts.
\[4~*~\frac{73}{100} = \boxed{2.92}\]
We will keep track of this approximation as we increase
the amount of throws (n). As we increase N, we might begin to notice something
astonishing.
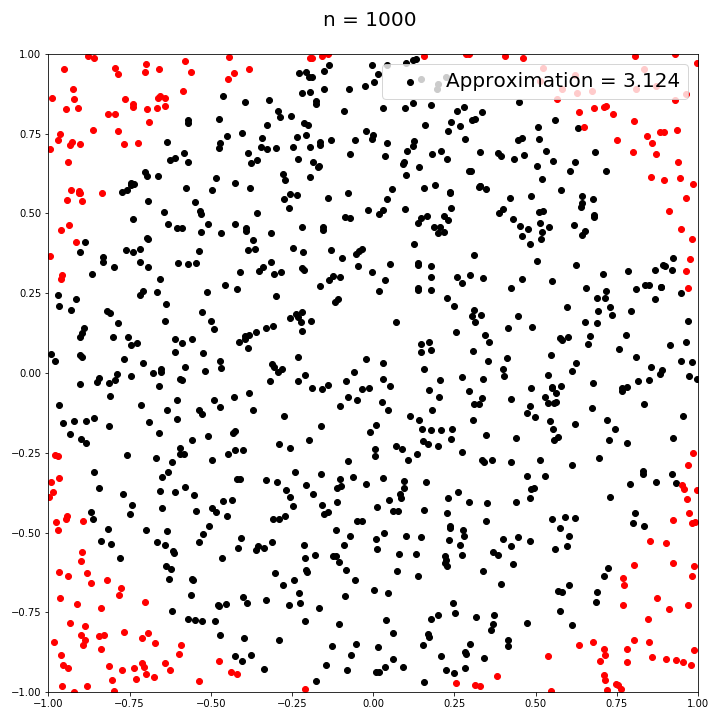

As we can see, as n increases, it seems like the proportion of hits and total attempts (multiplied by 4) seems to getting closer and closer to pi! In fact, we can see what happens to our approximation as n gets larger and larger.
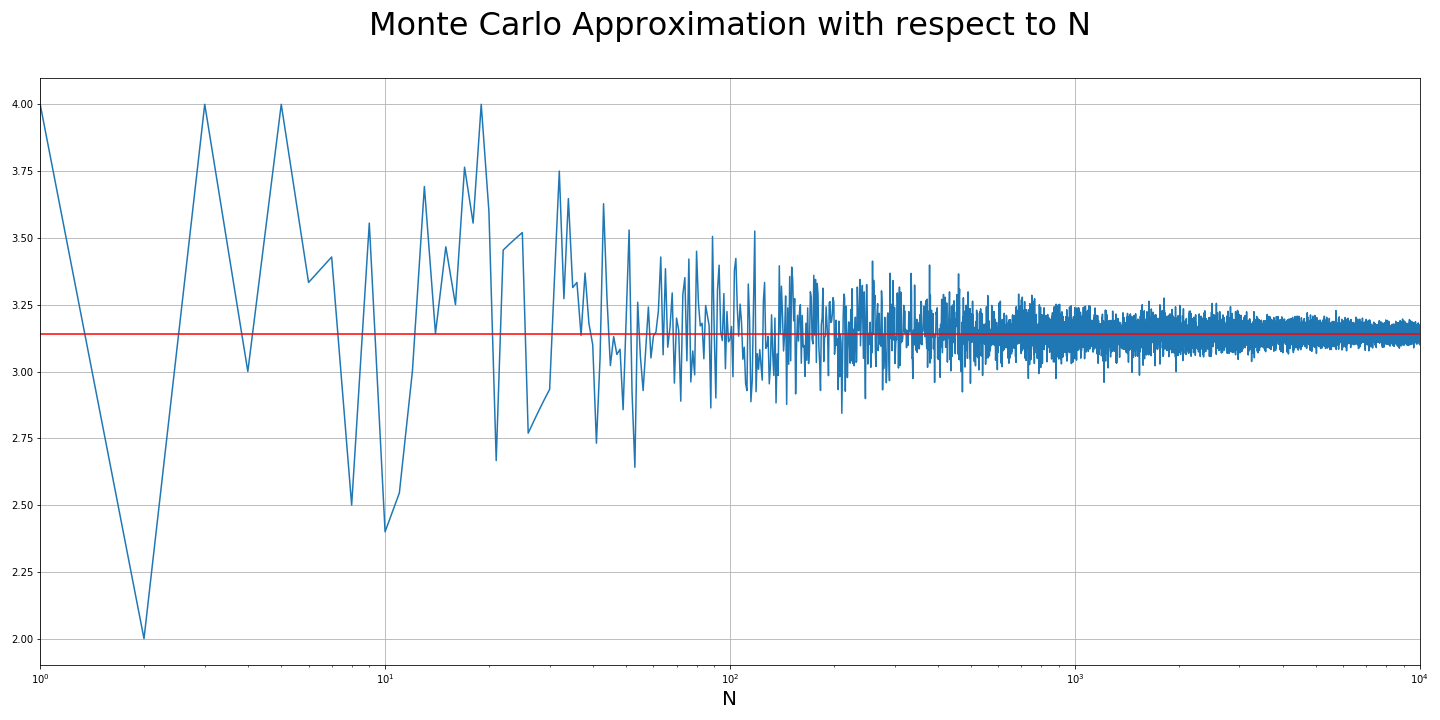
As the number of attempts increases, we can see that our approximation begins to converge at around 3.14! I think that's really cool!
But why...
III. Some Math
When we take a step back, we recall that to find this approximation, we are getting the proportion of attempts that landed within
the circle and dividing it by the misses. If we assume that there were a large amount of attempts taken to the point where the
entire board is covered, we can then think of the proportion as simply the area of the circle, divided by the area of the outer square.
\[Area~of~circle~=~ \pi r^2\]
\[Area~of~square~=~ lw = (2r)^2\]
\[\frac{\pi r^2}{(2r)^2}\]
\[\frac{\pi r^2}{4r^2}\]
\[\frac{\pi}{4}\]
Isn't that beautiful?
So essentially this tells us that if we were take an infinite amount of throws at this dartboard and take the proportion after we take those infinite throws, we would get pi! Time to start throwing!